Что такое
фрактал?
Фракталы – геометрические
объекты с дробной размерностью. К примеру, размерность линии – 1, площади – 2,
объема – 3. У фрактала же значение размерности может быть между 1 и 2 или между
2 и 3. К примеру, фрактальная размерность скомканного бумажного шарика
приблизительно равна 2,5. В математике существует специальная сложная формула
для вычисления размерности фракталов. Разветвления трубочек трахей, листья на
деревьях, вены в руке, река - это фракталы. Говоря простым языком, фрактал -
это геометрическая фигура, определенная часть которой повторяется снова и
снова, изменяясь в размерах - это и есть принцип самоподобия. Фракталы подобны
самим себе, они похожи сами на себя на всех уровнях (т.е. в любом масштабе).
Существует много различных типов фракталов. В принципе, можно утверждать, что
всё, что существует в реальном мире, является фракталом, будь то облако или
молекула кислорода.
Слово «хаос» наводит на
мысли о чем-то непредсказуемом, но на самом деле хаос достаточно упорядочен и
подчиняется определенным законам. Цель изучения хаоса и фракталов - предсказать
закономерности, которые, на первый взгляд, могут казаться непредсказуемыми и
абсолютно хаотическими.
Пионером в этой области познания
был франко-американский математик, профессор Бенуа Б. Мандельброт. В середине
1960-х им разработана фрактальная геометрия, целью которой был анализ ломаных,
морщинистых и нечетких форм. Множество Мандельброта (показано на рисунке) -
первая ассоциация, возникающая у человека, когда он слышит слово «фрактал». К
слову, Мандельброт определил, что фрактальная размерность береговой линии
Англии составляет 1,25.
Фракталы находят всё большее
применение в науке. Они описывают реальный мир даже лучше, чем традиционная
физика или математика. Броуновское движение - это, например, случайное и
хаотическое движение частичек пыли, взвешенных в воде. Этот тип движения,
возможно, является аспектом фрактальной геометрии, имеющий наибольшее
практическое использование. Случайное броуновское движение имеет частотную характеристику,
которая может быть использована для предсказания явлений, включающих большие
количества данных и статистики. К примеру, Мандельброт предсказал при помощи
броуновского движения изменение цен на шерсть.
Наиболее полезным
использованием фракталов в компьютерной технике является фрактальное сжатие
данных. При этом картинки сжимаются гораздо лучше, чем это делается обычными
методами - до 600:1. Другое преимущество фрактального сжатия в том, что при
увеличении не наблюдается эффекта пикселизации, резко ухудшающего картинку.
Мало того, фрактально сжатая картинка после увеличения часто выглядит даже
лучше, чем до него. Cпециалистам в области компьютерной техники известно также,
что фракталы бесконечной сложности и красоты могут быть сгенерированы простыми
формулами. Индустрия кино для создания
реалистичных элементов ландшафта (облака, скалы и тени) широко использует
технологию фрактальной графики.
Изучение турбулентности в
потоках очень хорошо подстраивается под фракталы. Это позволяет лучше понять
динамику сложных потоков. При помощи фракталов также можно смоделировать языки
пламени. Пористые материалы хорошо представляются в фрактальной форме в связи с
тем, что они имеют очень сложную геометрию. Для передачи данных на расстояния
используются антенны, имеющие фрактальные формы, что сильно уменьшает их
размеры и вес. Фракталы используются для описания кривизны поверхностей.
Неровная поверхность характеризуется комбинацией из двух разных фракталов.
На рисунке слева в качестве
простого примера приведен фрактал «пятиугольник Дарера», который выглядит, как
связка пятиугольников, сжатых вместе. Фактически он образован при использовании
пятиугольника в качестве инициатора и равнобедренных треугольников, отношение
большей стороны к меньшей в которых в точности равно так называемой золотой
пропорции (1.618033989 или 1/(2cos72°)) в качестве генератора. Эти треугольники
вырезаются из середины каждого пятиугольника, в результате чего получается
фигура, похожая на 5 маленьких пятиугольников, приклеенных к одному большому.
Теория хаоса говорит, что
сложные нелинейные системы являются наследственно непредсказуемыми, но, в то же
время утверждает, что способ выражения таких непредсказуемых систем оказывается
верным не в точных равенствах, а в представлениях поведения системы — в
графиках странных аттракторов, имеющих вид фракталов. Таким образом, теория
хаоса, о которой многие думают как о непредсказуемости, оказывается наукой о
предсказуемости даже в наиболее нестабильных системах. Учение о динамических
системах показывает: простые уравнения могут порождать такое хаотическое
поведение, при котором система никогда не возвращается в стабильное состояние и
при этом не проявляется никакой закономерности. Часто такие системы ведут себя
вполне нормально до некоторого определенного значения ключевого параметра,
потом испытывают переход, в котором существует две возможности дальнейшего
развития, потом четыре, и, наконец, хаотический набор возможностей.
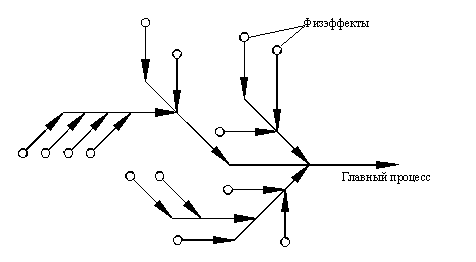Схемы процессов, протекающих
в технических объектах, имеют четко выраженное фрактальное строение. Структура
минимальной технической системы (ТС) подразумевает протекание в пределах ТС
двух типов процессов – главного и обеспечивающих, причем это деление условно и
относительно. Любой процесс может быть главным по отношению к обеспечивающим, а
любой из обеспечивающих процессов может считаться главным по отношению к
«своим» обеспечивающим процессам. Кружками на схеме обозначены физэффекты,
обеспечивающие протекание тех процессов, для обеспечения которых не требуется
специально создавать «свои» ТС. Эти процессы являются результатом
взаимодействия между веществами, полями, веществами и полями. Если быть точным,
то физэффект – это ТС, на принцип работы которой мы не можем повлиять, а в ее устройство
не желаем или не имеем возможности вмешиваться.
Протекание главного
процесса, изображенного на схеме, обеспечивается существованием трех
обеспечивающих процессов, являющихся главными для порождающих их ТС.
Справедливости ради отметим, что для функционирования даже минимальной ТС трех
процессов явно недостаточно, т.е. схема очень и очень утрирована.
Всё далеко не так просто,
как показано на схеме. Полезный (нужный человеку) процесс не может выполняться
со стопроцентной эффективностью. Рассеиваемая энергия затрачивается на создание
вредных процессов – нагрев, вибрации и т.п. В результате параллельно полезному
процессу возникают вредные. Не всегда есть возможность заменить «плохой»
процесс «хорошим», поэтому приходится организовывать новые процессы,
направленные на компенсацию вредных для системы последствий. Характерный пример
– необходимость борьбы с трением, вынуждающая организовывать хитроумные схемы
смазки, применять дорогостоящие антифрикционные материалы или затрачивать время
на смазку узлов и деталей или ее периодическую замену.
В связи с существованием
неизбежного влияния переменчивой Среды полезный процесс может нуждаться в
управлении. Управление может осуществляться как при помощи автоматических
устройств, так и непосредственно человеком. Схема процессов фактически является
набором специальных команд, т.е. алгоритмом. Сущность (описание) каждой команды
составляет совокупность отдельно взятого полезного процесса, сопутствующих ему вредных
процессов и набора необходимых управляющих процессов. В таком алгоритме набор
обеспечивающих процессов является обычной подпрограммой – и здесь мы тоже
обнаруживаем фрактал. Созданный четверть века назад метод Р.Коллера позволяет
при создании систем обойтись достаточно ограниченным набором всего из 12 пар
функций (процессов).
